|
Issue 1, Volume 7,
January 2008
Special Issue: Nonclassical
Lagrangian Dynamics and Potential Maps
Guest Editor: Constantin
Udriste
Title of the Paper: Euler-Lagrange
Characterization of Area-Minimizing Graphs in Randers Spaces
with Non-constant Potential
DOWNLOAD
FULL PDF
Authors: Vladimir Balan
Abstract: Within the framework of Randers spaces with non-constant
potential, the mean curvature form of hypersurfaces
is determined, and the equations which characterize the area-minimizing graph
surfaces are explicitly derived as associated Euler-Lagrange PDEs. By applying the extended framework to the particular
case of graphs in Randers spaces with constant
potential, the known result of Souza-Spruck-Tenenblat
([27]) is confirmed. It is shown that the only linear affine potentials for which the Randers metric
admits all the affine planes as minimal graphs, are necessarily constant. As
well, the ODE which characterizes the generating curve of surfaces of
revolution is derived, this extending the result obtained by Souza-Tenenblat in [26] in the constant potential case.
Keywords: Euler-Lagrange
equations, mean curvature 1-form, Finsler
structure, Randers
metric, hypersurfaces, minimal graphs, minimal
surfaces of revolution.
Title of the Paper: Necessary
Optimality Conditions for Fractional Action-Like Problems with Intrinsic and
Observer Times
DOWNLOAD
FULL PDF
Authors: Gastao
S. F. Frederico, Delfim
F. M. Torres
Abstract: We prove higher-order Euler-Lagrange and DuBois-Reymond
stationary conditions to fractional actionlike variational problems. More general fractional action-like
optimal control problems are also considered.
Keywords: calculus of
variations, FALVA problems, higher-order Euler-Lagrange equations,
higher-order DuBois-Reymond stationary condition,
multi-time control theory.
Title of the Paper: Non-Classical Lagrangian Dynamics and Potential Maps
DOWNLOAD FULL PDF
Authors: Constantin
Udriste
Abstract: The basic theory regarding Nonclassical Lagrangian Dynamics and Potential Maps was announced in
[7]. Since its mathematical impact is now at large vogue, we reinforce some
arguments. Section 1 extends the theory of harmonic and potential maps in the
language of differential geometry. Section 2 defines a generalized Lorentz world-force law and shows that any PDE system of
order one (in particular, p-flow) generates such a law in a suitable
geometrical structure. In other words, the solutions of any PDE system of
order one are harmonic or potential maps, i.e., they are solutions of
Euler-Lagrange prolongation PDE system of order two built via Riemann-
Lagrange structures and a least squares Lagrangian.
Section 3 formulates open problems regarding the geometry of semi-Riemann
manifolds (J1(T,M), S1), (J2(T,M), S2). Section 4
shows that the Lorentz-Udriste world-force law is
equivalent to certain covariant Hamilton PDEs on (J1(T,M), S1). Section 5 describes the maps determining a
continuous group of transformations as ultra-potential maps.
Keywords: ultra-harmonic
map, ultra-potential map, Lagrangian, Hamiltonian, Lorentz-Udriste world force law.
Title of the Paper: Euler-Lagrange-Hamilton
Dynamics with Fractional Action
DOWNLOAD
FULL PDF
Authors: Constantin
Udriste, Dumitru Opris
Abstract: Our aim is three-fold: to point out that the fractional integral
actions are coming from Stieltjes actions, to find
the roots and the geometry of some Euler-Lagrange or Hamilton ODEs or PDEs, to evidentiate some ideas that include the fractal theory of
solids. Section 1 discusses the Euler-Lagrange ODEs
associated to single-time Stieltjes actions. Their dual Hamilton ODEs are analized in Section 2. Section 3 studies the geometry
associated to singletime Euler-Lagrange or
Hamilton operators.
Section 4 analyzes the Euler-Lagrange PDEs
associated to multitime Stieltjes
actions (multiple or curvilinear integrals). Section 5 formulates the multitime perimetric problem of
nonrenewable resources. Section 6 studies the Hamilton PDEs
associated to multitime Stieltjes
actions. Section 7 describes the geometry associated to multitime
Euler-Lagrange or Hamilton
operators (dynamical connection and semi-spray, Poincare-Cartan
form, Hamilton-Poisson systems on jet bundle). Section 8 formulates a multitime Hamilton-Poisson systems theory on jet bundle.
Keywords: fractional Stieltjes action, Euler-Lagrange or Hamilton equations,
dynamic connection, symplectic manifold.
Title of the Paper: Nonclassical
Electromagnetic Dynamics
DOWNLOAD
FULL PDF
Authors: Constantin
Udriste, Dorel Zugravescu, Florin
Munteanu
Abstract: Our paper is concerned with effects of special forces on the motion
of particles. §1(§2) studies the singletime
geometric dynamics induced by electromagnetic vector fields (1-forms) and by
the Euclidean structure of the space. §3 defines the
second-order forms or vectors. §4 (§5) describes a nonclassical
electric (magnetic) dynamics produced by an ”electric
(magnetic) second-order Lagrangian”, via the extremals of the energy functional. §6 generalize this
dynamics for a general second-order Lagrangian,
having in mind possible applications for dynamical systems coming from
Biomathematics, Economical Mathematics, Industrial Mathematics, etc.
Keywords: geometric
dynamics, second-order vectors, second-order Lagrangian,
nonclassical dynamics.
Title of the Paper: Determining a
Metric by Boundary Single-Time Flow Energy
DOWNLOAD
FULL PDF
Authors: Ariana
Pitea
Abstract: Our theory of determining a tensor by single-time flow energy is
similar to those developed by Sharafutdinov.
Section 1 refines the theory of potential curves determined by a flow and a
Riemannian metric. Section 2 defines the boundary energy of a potential curve
and proves that the problem of determining a metric from a
single-time flow boundary energy cannot have a unique solution.
Section 3 linearizes the above-mentioned problem
and defines the notion of single-ray transform.
Keywords: potential
curves, least squares Lagrangian, single-ray transform,
boundary energy.
Title of the Paper: Determining a Pair
of Metrics by Boundary Energy Associated to a Multitime
PDE System
DOWNLOAD
FULL PDF
Authors: Ariana
Pitea, Constantin Udriste
Abstract: Our theory of determining a tensor by boundary energy of a multitime first order PDE system is similar to those
developed by Sharafutdinov. Section 1 refines the
theory of potential maps determined by a first order multitime
PDE system and a vertical metric. Section 2 defines the boundary energy of a
first order PDE system and proves that the problem of determining a vertical
metric from the boundary energy of a multitime PDE
system cannot have a unique solution. Section 3 linearizes
the above mentioned problem and defines the notion of multi-ray transform.
Keywords: potential map,
least squares Lagrangian, boundary energy,
multi-ray transform, extremals.
Title of the Paper: Multitime
Models of Optimal Growth
DOWNLOAD
FULL PDF
Authors: Constantin
Udriste, Massimiliano
Ferrara
Abstract: Section 1 underlines the limitations of standard multi-variable variational calculus and the sense of multitime.
Section 1 formulates the controllability problem for a multiple integral
functional or for a path independent curvilinear integral subject to a multitime evolution of flow type. Section 2 describes a
two-time optimal economic growth modelled by
Euler-Lagrange PDEs associated to a double integral
functional or to a path independent curvilinear integral in two dimensions.
Section 3 motivates the optimal economic growth by two-time maximum
principles. Section 4 studies the two-time optimal economic growth with
bang-bang policy based on a curvilinear integral action.
Keywords: multitime maximum principle, multitime
optimal economic growth, bang-bang policy.
Title of the Paper: A Descent Method
for Nonsmooth Variational
Inequalities via Regularization
DOWNLOAD
FULL PDF
Authors: Barbara Panicucci,
Massimo Pappalardo, Mauro Passacantando
Abstract: In this paper we propose a descent method for solving variational inequality problems where the underlying
operator is nonsmooth, locally Lipschitz,
and monotone over a closed, convex feasible set. The idea is to combine a
descent method for variational inequality problems
whose operators are nonsmooth, locally Lipschitz, and strongly monotone, with the Tikonov-Browder regularization technique. Finally,
numerical results are presented and discussed.
Keywords: variational inequality, nonsmooth
mapping, gap function, descent method, Tikhonov-Browder
regularization.
Title of the Paper: Generalized Multitime Lagrangians and
Hamiltonians
DOWNLOAD
FULL PDF
Authors: Constantin
Udriste, Paul Popescu,
Marcela Popescu
Abstract: We establish a natural frame for affine Lagrangians
and Hamiltonians. The focus is on the Hamiltonians applicable in classical
fields and their generalizations. A unitary treatment of scalar and
volume-valued Hamiltonians in a special class is obtained. Considering a variational problem of the action defined by a
Hamiltonian in this class, one obtains informations
about the multitime dynamical solutions of the
classical variational problem for scalar and
volume-valued Hamiltonians.
Keywords: affine lagrangian, affine hamiltonian,
variational equation, jet space.
Issue 2, Volume 7,
February 2008
Title of the Paper: Theoretical
Analysis of Inverse Weibull Distribution
DOWNLOAD
FULL PDF
Authors: M. Shuaib
Khan, G. R. Pasha, Ahmed Hesham
Pasha
Abstract: In this study we present the theoretical analysis of Inverse weibull distribution. This paper presents the flexibility
of the Inverse weibull distribution that approaches
to different distributions. Here we compare the relevant parameters such as
shape, scale parameters by using simulation analysis. Here we present the
relationship between shape parameter and other properties such as mean,
median, mode, variance, coefficient of variation, coefficient of skewness and coefficient of kurtosis models are shown
graphically and mathematically presented.
Keywords: Inverse weibull distribution, simulation analysis, graphically
analysis
Title of the Paper: An Lω1ω1 Axiomatization of the Linear Archimedean Continua as
Merely Relational Structures
DOWNLOAD
FULL PDF
Authors:
Milos Arsenijevic, Miodrag Kapetanovic
Abstract: We have chosen the language Lω1ω1 in which to formulate
the axioms of two systems of the linear Archimedean continua – the
point-based system, SP, and the stretch-based system, SI – for the following
reasons: 1. It enables us to formulate all the axioms of each system in one
and the same language; 2. It makes it possible to apply, without any
modification, Arsenijević's two sets of rules
for translating formulas of each of these systems into formulas of the other,
in spite of the fact that these rules were originally formulated in a
first-order language for systems that are not continuous but dense only; 3.
It enables us to speak about an infinite number of elements of a continuous
structure by mentioning explicitly only denumerably
many of them; 4. In this way we can formulate not only Cantor's coherence
condition for linear continuity but also express the large-scale and
small-scale variants of the Archimedean axiom without any reference, either
explicit or implicit, to a metric; 5. The models of the two axiom systems are
structures that need not be relational-operational but only relational, which
means that we can speak of the linear geometric continua directly and not
only via the field of real numbers (numbers will occur as subscripts only, and
they will be limited to the natural numbers).
Keywords: Linear
continuum, L_omega_1/omega_1, point-based, stretch-based axiomatization,
trivial difference, Archimedean axiom
Title of the Paper: Bifurcation
Diagrams of Generic Families of Singular Systems under Proportional and
Derivative Feedback
DOWNLOAD
FULL PDF
Authors: M. Isabel Garcia-Planas
Abstract: In this paper we study qualitative properties about nearby singular
systems using stratification method. We construct the stratification
partitioning the set of singular systems according to the complete set of
discrete invariants. We show that it is a constructible stratification and
that it is Whitney regular for one input regularizable
systems. We give an application to the obtention of
bifurcation diagrams for few parameter generic families of singular regularizable systems.
Keywords: Singular
systems, Feedback and derivative feedback equivalence, stratification,
canonical form, orbit, stratum.
Title of the Paper: Statistical
Analysis of a Nonstationary Fatigue Data Using the
ARIMA Approach
DOWNLOAD
FULL PDF
Authors: S. Abdullah, M. D. Ibrahim, A. Zaharim, Z. Mohd Nopiah
Abstract: Auto Regressive Integrated Moving Average (ARIMA) is a broad class
of time series models, and it has been achieved using the statistical
differencing approach. It is normally being performed using the computational
method. Thus, it is useful to choose the suitable model from a possibly large
selection of the available ARIMA formulations. The ARIMA approach was then analysed with the presence of stationary behaviour in a nonstationary
data. For the purpose of the random data analysis, a nonstationary
data that exhibiting a random behaviour was used.
This random data was measured in the unit of microstrain
on the lower suspension arm or a car travelling on
a country road surface. With this engineering unit, hence, the data is known
as a variable amplitude fatigue loading. Experimentally, the data was
collected for 225 seconds at the sampling rate of 200 Hz, which gave 45,000
discrete data points. Using the computational analysis by means of statistical
software package, the ARIMA parameters were estimated by the application of
the data smoothing technique in order to reduce the random variation of the
fatigue data. Therefore, the significant ARIMA parameters were established
and being applied in the study of the variation in nonstationary
data. For this paper, finally, it is suggested that the ARIMA method provided
a good platform to analyse fatigue random data,
especially in the scope of the durability research.
Keywords: ARIMA,
Statistical analysis, Fatigue, Nonstationary data,
Statistics.
Title of the Paper: An Evaluation of
Test Statistics for Detecting Level Change in BL(1,1,1,1) Models
DOWNLOAD
FULL PDF
Authors: Azami
Zaharim, Ibrahim Mohamed,
Shahrum Abdullah, Mohd.
Sahar Yahya
Abstract: A study is carried out to investigate the sampling properties of
the outlier test statistics of a procedure developed for detecting level
change in BL(1,1,1,1) processes. It is done with
respect to the sample size, the type of outlier and the size of the
coefficients of the BL(1,1,1,1) process. The results
show that, in general, the outlier detection procedure is capable of
detecting level change, although the performance is affected if ω is
large.
Keywords: Level change,
bilinear process, outlier test statistics, outlier detection procedure,
sampling properties.
Issue 3, Volume 7,
March 2008
Title of the Paper: On the Ermanno-Bernoulli and Quasi-Ermanno-Bernoulli
Constants for Linearizing Dynamical Systems
DOWNLOAD
FULL PDF
Authors: F. I. Arunaye,
H. White
Abstract: It is well known that the Ermanno-Bernoulli
constants derived from the Laplace-Runge-Lenz
vector of dynamical systems are efficiently used to reduce them to a system
of harmonic oscillator(s) and conservation law in the context of point and nonlocal symmetries of dynamical systems. In this paper,
we review Ermanno-Bernoulli constants and observe
that one can also use analogous constants obtained from the
Hamilton vector of dynamical systems to
serve the same purpose. We report the generic natural variables for reducing
such dynamical systems in two-dimensions and three-dimensions to a system of
one harmonic oscillator and two harmonic oscillators respectively, and a
conservation law with some examples. We also note that the symmetry groups
obtained from the reduced systems using the alternative constants are
realizations of those obtained from Ermanno-Bernoulli
constants. We also report here that the symmetries of the original dynamical
systems can be obtained from symmetries of the reduced systems.
Keywords: Quasi,
Constants, Symmetries, Vectors, Conservation, Oscillators, Laplace-Runge-Lenz, Hamilton,
Coordinates, Dynamical.
Title of the Paper: Qualitative
Properties of the Ice-Thickness in a 3D Model
DOWNLOAD
FULL PDF
Authors: S. N. Antontsev,
H. B. De Oliveira
Abstract: In this work we consider a 3D isothermal mathematical model for ice
sheets flows over a horizontal bedrock. The model is
derived from the mechanics and dynamics of ice sheets and experimental
results carried out in Glaciology. The final formulation of the model gives
rise to a degenerate quasi-linear elliptic-parabolic equation for the
ice-thickness function. Under appropriated initial and Dirichlet
boundary conditions, we discuss the existence and uniqueness of weak
solutions for this problem. Then, we prove that the local speed of
propagations of disturbances from the initial ice-thickness is finite. We
prove also that the solutions of this problem have the waiting-time local
behavior. To establish these properties we use here a suitable local energy
method.
Keywords: ice sheet
dynamics, existence, uniqueness, finite speed of propagations, waiting time.
Title of the Paper: Ultra Long Orbital
Tethers Behave Highly Non-Keplerian and Unstable
DOWNLOAD
FULL PDF
Authors: Radu
D. Rugescu, Daniele Mortari
Abstract: Large twin tethers are investigated as possible competitive-cost
tools for non-gasdynamic descent, landing, takeoff and return from target celestial bodies and as
passive tools for debris retrieval from orbit. The particular behavior of
orbiting bodies connected with long cables is a recent preoccupation in astrodynamics and proves being full of unexpected
results. The investigation here presented is focused on the non-Keplerian behavior of such large tether systems,
considered in a first approximation as rigid or very stiff and massless. The investigation starts with the feasibility
of non-gasdynamic orbital deployment of twin
tethers without any involvement of expensive rocket propulsion means. The
free tether release systems are associated to a horizontal impulsive
separation (HIS) and eventual friction-free deployment to the desired length.
This horizontal deployment seems to supply the most productive means of
continuous separation and departure of masses in orbit. The relative motion
during separation is studied and the observation is made that a considerable
kinetic moment of the system preserves during all eventual phases of the
flight. After the friction-free deployment the extending cable is instantly
immobilized at the so-called connection moment. From here after the tether
length remains constant. The evolution of the deployed tether is followed in
order to record the specific behavior when the length of the tether is
extremely great. The motion of the two connected masses and of the mass
center proves completely non-Keplerian, beginning
with the libration around local vertical due to the
considerable residual kinetic moment at connection. A practical application
of the quasi-vertical libration is in orbital
passive debris collector, when a sandwich composite large panel is orbited
for long periods of time for collecting small mass, high velocity Earth orbit
debris. The most promising and controversial application of such long tethers
resides in the anchoring technique to achieve the skeleton of a future space
elevator. The stability of motion is an important aspect which is approached
my numerical simulations.
Keywords: Astrodynamics, Space tethers, Tether dynamics, Large
space structures, Tether instability.
Title of the Paper: Implications of a
Scale Invariant Model of Statistical Mechanics to Nonstandard Analysis and
the Wave Equation
DOWNLOAD
FULL PDF
Authors: Siavash
H. Sohrab
Abstract: A scale-invariant model of statistical mechanics is applied to examine
the physical foundation of nonstandard analysis and to identify the nature
and the range (0β, 0β−1) of nonstandard
numbers and to establish the existence of infinitesimals (0β
> Lβ−2 > xβ
> 0β−2). An invariant logarithmic definition of
coordinate is presented and the concept of “measureless” or “dimensionless”
numbers (L’β, λβ,
0β) = (Lβ, 1β,
0β) is described. Also, a scale-invariant definition of
fractal dimension is introduced that suggest exceedingly large values 107
of fractal dimension. A scale invariant form of the wave equation is derived
that applies to acoustic waves that propagate at speed of sound vm = 350 m/s, gravitational waves that
propagate at the speed of light vt = c,
and gravitational radiation that propagates at superluminal speeds vg
> 2 x1010 c.
Keywords: Nonstandard
analysis; Infinitesimals; Gravitational waves; Gravitational radiation.
Title of the Paper: Fuzzy Approach to
Semi-Parametric of a Sample Selection Model
DOWNLOAD
FULL PDF
Authors: L. Muhamad
Safiih, A. A. Basah Kamil, M. T. Abu Osman
Abstract: The sample selection model is studied in the context of
semi-parametric methods. With the deficiency of the parametric model, such as
inconsistent estimators etc, the semi-parametric estimation methods provide
the best alternative to handle this deficiency. Semi-parametric of a sample
selection model is an econometric model and has found interesting application
in empirical studies. The issue of uncertainty and ambiguity still become are
still major problem and are complicated in the modelling
of a semi-parametric sample selection model as well as its
parametric. This study, focuses on the context of
fuzzy concept as a hybrid to the semi-parametric sample selection model. The
best approach of accounting for uncertainty and ambiguity is to take
advantage of the tools provided by the theory of fuzzy sets. It seems
particularly appropriate for modelling vague
concepts. Fuzzy sets theory and its properties, through the concept of fuzzy
number, provide an ideal framework in order to solve the problem of uncertain
data. In this paper, we introduce a fuzzy membership function for solving
uncertain data of a semi-parametric sample selection model.
Keywords: uncertainty,
semi-parametric sample selection model, crisp data, fuzzy number, membership
function
Title of the Paper: Fuzzy
Semi-Parametric Sample Selection Model Case Study for Participation of
Married Women
DOWNLOAD
FULL PDF
Authors: L. Muhamad
Safiih, A. A. Basah Kamil, M. T. Abu Osman
Abstract: The sample selection model is studied in the context of semi-parametric
methods. The issue of uncertainty and ambiguity are still major problems and
the modelling of a semi-parametric sample selection
model as well as its parametric. The best approach
of accounting for uncertainty and ambiguity is to take advantage of the tools
provided by the theory of fuzzy sets. The semi-parametric of a sample
selection model is an econometric model that has found an interesting
application in empirical studies. In this paper, the married women
participants in the Malaysia
labour force are studied. It comprises the analysis
of a) participation equation in the wage sector and b) the wage equation in
the wage sector. The data set used for this study is from the Malaysian
population and family survey 1994 (MPFS-1994).
Keywords: uncertainty,
semi-parametric sample selection model, participant equation, wage equation,
fuzzy number.
Issue 4, Volume 7,
April 2008
Title of the Paper: The Stability of
Collocation Methods for Approximate Solution of Singular Integro-
Differential Equations
DOWNLOAD
FULL PDF
Authors: Iurie
Caraus, Nikos E. Mastorakis
Abstract: In this article we obtained that the collocation methods are stable
in according with the small perturbations of coefficients, kernels and right
part of studied equations. We proved that the condition number of the
approximate operator exists and bounded. The condition number of collocation
methods is appropriated with condition number for exact singular integro- differential equations.
Keywords: condition
number, stability, collocation methods, singular integro-
differential equations.
Title of the Paper: Optimal Operational
Strategy for Hybrid Renewable Energy System Using Genetic Algorithms
DOWNLOAD
FULL PDF
Authors: Kamaruzzaman
Sopian, Azami Zaharim, Yusoff Ali,
Zulkifli Mohd Nopiah, Juhari Ab. Razak, Nor Salim Muhammad
Abstract: Off-grid settlements require efficient, reliable and cost-effective
renewable energy as alternative to the power supplied by diesel generator.
Techno-economic analysis is required to find the optimum renewable energy
system in the long run. This paper reviews the application of genetic
algorithms in optimization of hybrid system consisting of pico
hydro system, solar photovoltaic modules, diesel generator and battery sets.
It is intended to maximize the use of renewable system while limiting the use
of diesel generator. Daily load demand is assumed constant for derivation of
annual load. Power derived from the hybrid should be able to meet the demand.
Local weather data is used and analyzed to assess the technical and economic
viability of utilizing the hybrid system. Optimization of the system will be
based on the component sizing and the operational strategy. Genetic
algorithms programming is used to evaluate both conditions in minimizing the
total net present cost for optimum configuration. Manufacturer data for the
hybrid components is used in calculation of sizing to represent actual power
derivation. Several operation strategies will be considered while forming the
vectors for optimum strategy. Random selection of sizing and strategy is used
to initiate the solution for the problem which will have the lowest total net
present cost. Sensitivity analysis is also performed to optimize the system
at different conditions.
Keywords: Genetic
algorithms; Operation strategy; Hybrid system; Renewable energy, Optimization
Title of the Paper: Improved Estimation
of State of Stochastic Systems via Invariant Embedding Technique
DOWNLOAD
FULL PDF
Authors: Nicholas A. Nechval, Gundars Berzins, Maris Purgailis, Konstantin N. Nechval
Abstract: In the present paper, for constructing the minimum risk estimators
of state of stochastic systems, a new technique of invariant embedding of
sample statistics in a loss function is proposed. This technique represents a
simple and computationally attractive statistical method based on the
constructive use of the invariance principle in mathematical statistics.
Unlike the Bayesian approach, an invariant embedding technique is independent
of the choice of priors. It allows one to eliminate unknown parameters from
the problem and to find the best invariant estimator, which has smaller risk
than any of the well-known estimators. Also the problem of how to select the
total number of the observations optimally when a constant cost is incurred
for each observation taken is discussed. To illustrate the proposed
technique, examples are given.
Keywords: Stochastic
system; State; Estimation; Invariant embedding technique
Title of the Paper: Identification of a
Heat Transfer Coefficient when it is a Function Depending on Temperature
DOWNLOAD
FULL PDF
Authors:
Andres
Fraguela, Juan–Antonio Infante,
Angel Manuel Ramos, Jose
Maria Rey
Abstract: This paper deals with an inverse problem concerning the
identification of the heat exchange coefficientH
(assumed depending on the temperature) between a certain material with the
external environment (see, e.g., [12], [20] for real applications modelled with equations involving this coefficient). Only
experimental measurements of the temperature are supposed to be known. The
goal is to identifyH in order to get a solution for
the corresponding model, approximating some given temperature measurements.
The main difficulty is that we consider the case of functions H depending on
the solution of the state equation. We begin by setting several scenarios for
the inverse problem. For each scenario, we know the initial and ambient
temperatures, we identify function H through different methods and we obtain
error bounds in adequate norms (uniform and square integrable).
Finally, we study the inverse problem in the framework of the classical
theory for Hilbert spaces. Several methods are used (Tikhonov,
Morozov, Landweber,. . . ) and the approximations obtained, as well as the one
provided by our method, are shown.
Keywords: Function
identification, Inverse Problems, Heat exchange, Regularization strategies.
Title of the Paper: Fast Algorithms and
MATLAB Software for Solution of the Dirichlet Boundary Value Problems for
Elliptic Partial Differential Equations in Domains with Complicated Geometry
DOWNLOAD
FULL PDF
Authors: Alexandre
Grebennikov
Abstract: New fast algorithms for solution of the Dirichlet boundary value problem for the class of
elliptic Partial Differential Equations (PDE) is proposed. Algorithms
are based on new version of General Ray (GR) method which consists in
application of the Radon transform directly to the PDE and in reduction PDE
to assemblage of Ordinary Differential Equations (ODE). The class of the PDE
includes the Laplace,
Poisson and Helmgoltz equations. GR-method presents
the solution of the Dirichlet boundary value
problem for this type of equations by explicit analytical formulas that use
the direct and inverse Radon transform. Proposed version of GR-method is
justified theoretically, realized by MATLAB software, which quality we
demonstrate by numerical experiments.
Keywords: fast
algorithms, boundary value problems , partial differential equations, Radon
transform, MATLAB software
Title of the Paper: Manufacturing Lot Sizing with Backordering, Scrap, and Random
Breakdown Occurring in Inventory-Stacking Period
DOWNLOAD
FULL PDF
Authors: Singa
Wang Chiu, Jyh-Chau Yang, Shu-Ying
Chen Kuo
Abstract: This paper is concerned with determination of optimal lot size for
an economic manufacturing quantity model with backordering, scrap and
breakdown occurring in inventory-stacking period. Generation of defective
items and random breakdown of production equipment are inevitable in most
real-life manufacturing systems. To cope with the stochastic machine
failures, production planners practically calculate the mean time between
failures (MTBF) and establish the robust plan accordingly, in terms of
optimal lot size that minimizes total production-inventory costs for such an
unreliable system. Random scrap rate is considered in this study, and
breakdown is assumed to occur in inventory stacking period. Mathematical
modeling and analysis is used and the renewal reward theorem is employed to
cope with the variable cycle length. An optimal manufacturing lot size that
minimizes the long-run average costs for such an imperfect system is derived.
Numerical example is provided to demonstrate its practical usages.
Keywords: Optimization,
Manufacturing systems, Production lot size, Machine breakdown, Backordering,
Scrap, Inventory
Title of the Paper: A Matricial Public Key Cryptosystem with Digital Signature
DOWNLOAD
FULL PDF
Authors: Rafael Alvarez,
Francisco-Miguel Martinez, Jose-Francisco Vicent,
Antonio Zamora
Abstract: We describe a new public key cryptosystem using block upper
triangular matrices with elements in Zp , based on a generalization of the discrete logarithm
problem over a finite group. The proposed cryptosystem is very efficient,
requiring very few operations and also allows an ElGamal
based digital signature scheme. The main benefit is that the security level
is higher than other algorithms for the same key size.
Keywords: Cryptography,
Security, Public-Key, DLP, Finite Fields, Diffie-Hellman,
Polynomial Matrices, ElGamal, Digital Signature.
Issue 5, Volume 7,
May 2008
Title of the Paper: A Multistage
Mean/Variance Approach for Portfolio Management in the Mexican Market
DOWNLOAD
FULL PDF
Authors: Maria A. Osorio, Ana Ballinas, Erika Jimenez, Abraham
Sanchez
Abstract: This paper describes the use of Mean/Variance multistage portfolio
management for building efficient frontiers. The maximization of the returns
yields the maximum and the variance minimization the minimum points in the
efficient frontier. The efficient frontier is the graph describing all the
optimal options between these two points. The intermediate points are
obtained minimizing the variance (risk measure) subject to different
percentages of the maximum utility expected. According to the investor’s
characteristics, a point in the graph, containing a complete set of
investment strategies can be chosen. The stochastic quadratic and linear
models use a scenario tree to represent the multistage discretization
of the random returns. The examples are applied to the Mexican bursaries
market.
Keywords: Portfolio
Management, Stochastic Programming, Mean/Variance Optimization.
Title of the Paper: Incomplete
Linguistic Preference Relations to Evaluate Multimedia Authoring System
DOWNLOAD
FULL PDF
Authors: Tien-Chin
Wang, Ying-Hsiu Chen, Yu-Chen
Chiang
Abstract: MCMD problems with fuzzy preference information on alternatives are
essential problems of the importance of weighting and ranking. In this study,
the AHP method is reviewed, and then Fuzzy PreRa
and incomplete linguistic preference relations methods are elucidated. This
study applied above three MCDM methods to a software selection problem
proposed by Lai et al. [Software selection: a case study of the application
of the analytical hierarchical process to the selection of a multimedia
authoring system, Information and Management, Vol.36, 1999, pp.221-232.]. The
outcome obtained by Fuzzy PreRa and incomplete
linguistic preference relations methods almost coincides with that produced
by the AHP method, also with the least judgments. The result shows that the
approach developed is simple and comprehensible in concept, efficient in
computation, and robust in modeling human evaluation processes which make it
of general use for solving practical qualitative multi-criteria problems.
Keywords: AHP, fuzzy
preference relations, incomplete linguistic preference relations, multimedia
authoring system (MAS), multi-criteria decision making (MCDM), selection
Title of the Paper: Embedding a Family
of 2D Meshes into Mobius Cubes
DOWNLOAD
FULL PDF
Authors: Chia-Jui
Lai, Jheng-Cheng Chen
Abstract: M¨obius cubes are an important class of
hypercube variants. This paper addresses how to embed a family of disjoint 2D
meshes into a M¨obius
cube. Two major contributions of this paper are: (1) For n ≥ 1, there
exists a 2 × 2n−1 mesh that can be embedded in the n-dimensional M¨obius cube with dilation 1 and expansion 1. (2) For n ≥
4, there are two disjoint 4 × 2n−3 meshes that can be embedded in the
n-dimensional 0-type M¨obius cube with dilation 1.
The results are optimal in the sense that the dilations of the embeddings are
1. The result (2) mean that a family of two
2D-mesh-structured parallel algorithms can be operated on a same crossed cube
efficiently and in parallel.
Keywords: M¨obius cubes, mesh embedding, dilation, expansion,
interconnection network.
Title of the Paper: Numerical Modeling
of Mild Slope Equation with Finite Volume Method
DOWNLOAD
FULL PDF
Authors: Asu
Inan, Lale Balas
Abstract: When waves propagate from deep water to shallow water, they
transform. Extended mild slope equation includes wave transformations such as
refraction, diffraction, shoaling, reflection and dissipations due to bottom
friction and wave breaking and harbour resonance.
Extended mild slope equation can be applied to the rapidly varying
topographies through higher order bottom effetcs.
Nonlinear wave celerity and group velocity have been considered in the
calculations. In this study, extended mild slope equation has been reduced to
Helmholtz equation and solved with finite volume
method. Numerical model has been tested on semicircular shoaling area and
compared with the physical experiment measurements given in literarure. Numerical model has been applied to the
Fethiye
Bay in the Mediterranean Sea in Turkey.
Keywords: Extended mild
slope equation, finite volume method, wave refraction, diffraction, nonlinear
wave celerity and group velocity
Title of the Paper: Varadhan
Estimates without Probability: Upper Bound
DOWNLOAD
FULL PDF
Authors: Remi
Leandre
Abstract: We translate in semi-group theory our proof of Varadhan
estimates for subelliptic Laplacians
which was using the theory of large deviations of Wentzel-Freidlin
and the Malliavin Calculus of Bismut
type.
Keywords: Large
deviations. Subelliptic estimates.
Title of the Paper: Global Optimization
using Hybrid Approach
DOWNLOAD
FULL PDF
Authors: Ting-Yu Chen, Yi Liang Cheng
Abstract: The paper deals with a global optimization algorithm using hybrid
approach. To take the advantage of global search capability the evolution
strategy (ES) with some modifications in recombination formulas and elites
keeping is used first to find the near-optimal solutions. The sequential
quadratic programming(SQP) is then used to find the
exact solution from the solutions found by ES. One merit of the algorithm is
that the solutions for multimodal problems can be found in a single run.
Eight popular test problems are used to test the proposed algorithm. The
results are satisfactory in quality and efficiency.
Keywords: Global
optimization algorithm, hybrid approach, evolution strategy
Title of the Paper: Weights,
Inequalities and a Local Holder Norm for Solutions to (∂/∂t-L)(u)=divf on
Bounded Domains
DOWNLOAD
FULL PDF
Authors: Caroline Sweezy
Abstract: The rate of change of u, a solution to Lu=divf
in a bounded, rough domain ΩT, u=g on ∂pΩT , is investigated
using a local Hölder norm of u and different
measures on ΩT and on ∂pΩT. Results
are discussed for both L a strictly elliptic operator and for L=∂/∂t-L0,
with L0 a strictly parabolic divergence form operator; the coefficients are
bounded and measurable, and in the case of L0 , time
dependent.
Keywords: elliptic,
parabolic equations, Lipschitz domains, Borel measures, kernels, Hölder
norms.
Title of the Paper: The Asymptotical
Behavior of Probability Measures for the Fluctuations of Stochastic Models
DOWNLOAD
FULL PDF
Authors: Jun Wang, Cuining Wei
Abstract: We consider the fluctuations of shapes of two phases
boundaries of the one-dimensional statistical mechanics models. By applying
the theory of one-dimensional random walk, the models of the two phases boundaries are constructed by assuming that there
is a specified value of the large area in the intermediate region of the two
phases boundaries. Then we investigate the asymptotical behavior of the
corresponding sequence of probability measures describing the statistical properties
of the two phases boundaries. We show that the
limiting probability measures coincide with some conditional probability
distribution of certain Gaussian distribution. Further we discuss the
properties of fluctuations of phase separation lines for the Ising model, and we obtain the asymptotic properties of
the two interfaces S.O.S. model.
Keywords: Stochastic
models; random phase boundaries; central limit theory; random walk; Gibbs
measure; Hamiltonian
Title of the Paper: The Analysis and
Correction of Factors Influencing Imaging Quality of Digital Radiographic
Testing System
DOWNLOAD
FULL PDF
Authors: Cheng Yao-Yu,
Li Yong-Hong , Hu Yan,
Liu Yan-Hua
Abstract: The factors influencing imaging quality of industrial digital
radiographic imaging system are analyzed detailedly.
This imaging system is a new type industrial digital radiographic imaging
system developed by author, The structure of ray conversion screen and its
non-uniformity, the discordance analysis of scientific grade CCD and vignetting effect of the optical system are introduced.
The correction method of non-uniformity for testing system is studied, the
correction arithmetic is given and the methods of reducing circuit random
noise and the noise produced by scatter ray are illuminated. The correction
image and the one that don’t be corrected are given, the merits of this
system and problem need to be more studied are illuminated.
Keywords: digital radiographic
imaging, non-uniformity correction, x ray conversion, scientific grade CCD,
dark current
Title of the Paper: Combinatorial
Optimization: Mutual Relations among Graph Algorithms
DOWNLOAD
FULL PDF
Authors: Eva Milkova
Abstract: The Theory of Graphs is a wonderful, practical discipline.
Informatics has played a big part in its development, and these two fields
are strongly interconnected. This can, perhaps, mainly be seen in the design
of computer algorithms. On the one hand, there are many methods which can be
used for solving the same problem, while on the other hand, using effective
modifications of one algorithm, we can devise methods of solving various
other tasks. To educate students in the area close connected with Graph
Theory and Computer Science, called as Combinatorial or Discrete
Optimization, it is important to make them familiar with certain algorithms
in contexts to be able to get deeper into each problem and entirely
understand it. In the paper we present just a few ideas that have proved
successful in teaching and learning this quite young part of mathematics.
Keywords: Graph
Algorithms, Minimum Spanning Tree Problem, Breadth-First-Search, Depth-First-Search,
Dijkstra’s Algorithm, Maze Problem, Eulerian Graph
Title of the Paper: Investigation of
Characteristics of Separation Zones in T-Junctions
DOWNLOAD
FULL PDF
Authors: Hamid
Shamloo, Bahareh Pirzadeh
Abstract: The river diversion, for domestic, agricultural and industrial
consumption, has a vital role to make economic progress and to develop the
human communities. There are different ways of river diversion which are
proportional to rivers' condition and the quantity of the diversion of water.
Lateral river intake is one of these ways. This paper provides detail
application of FLUENT-2D software in simulation of lateral intake flows.
Numerical simulations undertaken in present two dimensional work use RSM
turbulent model. Results of velocity field measurement using K-e Standard
model were compared with Shettar & Murthy
(1966). Then using RSM turbulent model, dimensions of separation zone were
measured and compared with Kasthuri & Pundarikanthan (1987). In both cases good agreement are
found between numerical and experimental results.
Keywords: Open channel,
Lateral Intake, Turbulence, Separation zone, Numerical modeling, Fluent
Title of the Paper: Bifuzzy
Ideals of K-Algebras
DOWNLOAD
FULL PDF
Authors: Muhammad Akram
Abstract: In this paper we introduce the notion of bifuzzy
ideals of K-algebras and investigate some interesting properties. Then we
study the homomorphisms between the ideals of
K-algebras and their relationship between the domains and the co-domains of
the bifuzzy ideals under these homomorphisms.
Finally the Cartesian product of bifuzzy ideals is
discussed.
Keywords: Bifuzzy ideals; Characteristic; Equivalence relations; Homomorphisms; Cartesian product.
Title of the Paper: A
Note on the Modified Hermitian and Skew-Hermitian Splitting Methods for Non-Hermitian
Positive Definite Linear Systems
DOWNLOAD
FULL PDF
Authors: Shi-Ling Wu, Ting-Zhu Huang
Abstract: Comparing the lopsided Hermitian/skew-Hermitian
splitting (LHSS) method and Hermitian/skew-Hermitian
splitting (HSS) method, a new criterion for choosing the above two methods is
presented, which is better than that of Li, Huang and Liu [Modified Hermitian and skew-Hermitian
splitting methods for non-Hermitian
positive-definite linear systems, Numerical Lin. Alg.
Appl., 14 (2007): 217-235].
Keywords: non-Hermitian matrix; splitting; skew-Hermitian
matrix; Hermitian matrix; iteration
Issue 6, Volume 7,
June 2008
Title of the Paper: Function
Approximation using Artificial Neural Networks
DOWNLOAD
FULL PDF
Authors: Zarita
Zainuddin, Ong
Pauline
Abstract: Function approximation, which finds the underlying relationship
from a given finite input-output data is the
fundamental problem in a vast majority of real world applications, such as
prediction, pattern recognition, data mining and classification. Various
methods have been developed to address this problem, where one of them is by
using artificial neural networks. In this paper, the radial basis function
network and the wavelet neural network are applied in estimating periodic,
exponential and piecewise continuous functions. Different types of basis
functions are used as the activation function in the hidden nodes of the
radial basis function network and the wavelet neural network. The performance
is compared by using the normalized square root mean square error function as
the indicator of the accuracy of these neural network models.
Keywords: function
approximation, artificial neural network, radial basis function network,
wavelet neural network.
Title of the Paper: Two Congruence
Classes for Symmetric Binary Matrices over F2
DOWNLOAD
FULL PDF
Authors: Yong-Hyuk
Kim, Keomkyo Seo
Abstract: We provide two congruence classes for symmetric binary matrices
over a finite field of characteristic 2. We use standard methods of matrix
analysis to prove directly that there exist two congruence classes. Our proof
gives explicit algorithms to compute the congruence classes.
Keywords: congruence of
matrices, binary matrices, finite field of characteristic 2.
Title of the Paper: The Matrix Padé Approximation in Systems of Differential Equations
and Partial Differential Equations
DOWNLOAD
FULL PDF
Authors: C. Pestano-Gabino,
C. Gonzalez-Concepcion, M. C.
Gil-Farina
Abstract: In [3] we presented a technique to study the existence of rational
solutions for systems of linear firstorder ordinary
differential equations. The method is based on a rationality characterization
that involves Matrix Padé Approximants. Moreover
the main ideas were only applied in the numerical resolution of a particular
partial differential equation. This paper may be considered as an extension
of [3], in the sense that we propose fundamental matrices directly for linear
m-order ordinary differential equations without making a transformation to an
equivalent system of first order. In addition, we increase its field of
applications to particular solutions of the mentioned systems and to Partial
Differential Equations.
Keywords: Systems of
Differential Equations, Partial Differential Equations (PDE), Matrix Padé Approximation (MPA), rational solutions, minimum
degrees (m.d.)
Title of the Paper: A Functional
Approximation Comparison between Neural Networks and Polynomial Regression
DOWNLOAD
FULL PDF
Authors: Ong
Hong Choon, Leong Chee Hoong, Tai Sheue Huey
Abstract: Multi-layered perceptron (MLP) neural
networks are well known as universal approximators.
They are often used as estimation tools in place of the classical statistical
methods. The focus of this study is to compare the approximation ability of
MLP with a traditional statistical regression model, namely the polynomial
regression. Comparison among the single hidden layer MLP, double hidden layer
MLP and polynomial regression is carried out on the basis of similar number
of weights or parameters. The performance of these three categories is
measured using fraction of variance unexplained (FVU). The closer the FVU
value is to zero, the better the estimation result and this is associated
with a higher degree of accuracy. From the empirical results obtained in this
study, we conclude that overall polynomial regression performs slightly
better than MLP for a similar number of parameter except for the complicated
interaction function. Meanwhile, double hidden layer MLP outperforms single
hidden layer MLP. The MLP is more appropriate than the polynomial regression
in approximating the complicated interaction function.
Keywords: Artificial
neural network, Multi-layered perceptrons,
Polynomial regression
Title of the Paper: Exact Test Critical
Values for Correlation Testing with Application
DOWNLOAD
FULL PDF
Authors: Ching-Hui
Chang, Jyh-Jiuan Lin, Nabendu
Pal
Abstract: Tables of critical values for the exact test method based on the
maximum likelihood estimator (MLE) have been obtained to test a hypothesis on
the correlation coefficient between the components of a bivariate
normal random vector. The exact test is then compared, in terms of size and
power, with the other popular methods, namely - the ‘z - test’, the ‘modified
z - test’ and the ‘t - test’. While these popular
methods have almost identical size and power to the exact test for large
samples, their small sample performance is far from satisfactory as evident
from our extensive numerical computations. Thus, our tables of critical
values are useful when sample size is not large (i.e., ≤ 30 ). Also, it is demonstrated through a real-life dataset
how the tables of critical values can be used for interval estimation.
Keywords: Asymptotic
variance, confidence interval, size, power.
Title of the Paper: Improving
Probability Education Through Statistical Experiments
DOWNLOAD
FULL PDF
Authors: Saeed
Al-Hajjar
Abstract: This study analyze some hypothesis on the
difficulties facing the teaching of probabilities, and see how models of
probability are useful to solve any confusion. This will be clarified by
formulating questions that can be addressed with data, collect
, organize, and display relevant data to answer them. In this part we
will see the solution of the problem ” who will win
the million ”, which is a good example of improving probability education
through statistical experiments.
Keywords: Hazard,
Confirmed, Change, Probability, Modeling, Random Experiment, Equiprobable
Title of the Paper: The Local analytic
Solution to Some Nonlinear Diffusion-Reaction Problems
DOWNLOAD
FULL PDF
Authors: Gabriella Bognar, Erika Rozgonyi
Abstract: -The positive radially symmetric
solutions to the nonlinear problem
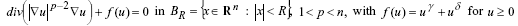
are considered. We
examine the existence of local solutions and give a method for the
determination of power series solutions. The comparison of the local analytic
and entire solutions is given for some special values of parameters p, n, γ, and δ.
Keywords: Nonlinear
partial differential equations, p-Laplacian,
non-Newtonian fluid, polytrophic gas, local analytic solutions
Title of the Paper: Stress Strain
Modeling by Transformed Equations of Ultrasonic Wave
DOWNLOAD
FULL PDF
Authors: Arash
Ziaie, Kaveh Kumarci, Arash Kyioumarsi
Abstract: The equations of ultrasonic wave propagation in Cartesian
coordinates are functions of 27 partial displacement derivatives, which first
derived and then transformed into cylindrical coordinates. The new obtained
functions are functions of 27 partial displacements of first and second order
derivatives in cylindrical coordinates too and they will be linearized using a perturbation method based on the
Taylor series
expansion. A displacement wave, which propagates in a body, composed of two
general part; static displacement part, and also small dynamic displacement
part. Happening of the small dynamic displacement of a particle around its
static situation, Taylor
series expansion can be written around this point. Using this determined
static situation and considering only the two first components of
Taylor series
expansion, the equations of motion will be linearized.
Tremendously lengthy algebraic operations involved in the derivation and
linearization process, all of the mathematical manipulations are performed using
Mathematica.
Keywords: perturbation- acoustoelasticity- strained cylindrical solids-
ultrasonic- wave propagation- Mathematica
Title of the Paper: On
the Ratio Processes Induced from the Mean-Field Bouchaud-Mezard Model
DOWNLOAD
FULL PDF
Authors: Feng-Rung
Hu
Abstract: In this article, we develop the ratio processes 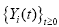 i=
1,2,...,n induced from the meanfield
Bouchaud-Mezard model. The limit i m of the long-time average of the ratio process i=
1,2,...,n induced from the meanfield
Bouchaud-Mezard model. The limit i m of the long-time average of the ratio process 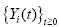 is
studied and compared with all others. We shows that a strictly increasing
sequence is
studied and compared with all others. We shows that a strictly increasing
sequence 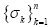 of the investment volatilities implies a strictly
decreasing sequence of the investment volatilities implies a strictly
decreasing sequence 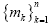 of the limits, given appropriate J, based on both
theoretical and numerical analyses. It reveals a negative correlation between
the investment volatilities and the ratio processes. As an empirical
application, this negative correlation can be employed to characterize the
mean-field Bouchaud-Mezard model. Our main result
also indicates that an agent whose spontaneous growth or decrease in wealth
due to investment in stock markets is always small will eventually become
rich in the meanfield Bouchaud-Mezard
model. of the limits, given appropriate J, based on both
theoretical and numerical analyses. It reveals a negative correlation between
the investment volatilities and the ratio processes. As an empirical
application, this negative correlation can be employed to characterize the
mean-field Bouchaud-Mezard model. Our main result
also indicates that an agent whose spontaneous growth or decrease in wealth
due to investment in stock markets is always small will eventually become
rich in the meanfield Bouchaud-Mezard
model.
Keywords: Mean-field Bouchaud-Mezard model, Wealth distribution, Ratio
process, Volatility, Ergodic, Long-time average
Title of the Paper: The
Influence of the Geometry and the Material Properties on the Behavior of the
Human Knee
DOWNLOAD
FULL PDF
Authors: Valerica
Mosnegutu, Veturia Chiroiu Lucian Capitanu, Mihai Popescu
Abstract: In this paper, the motion of the knee joint during flexion and
extension is investigated. It is developed a mathematical model of the knee
joint that describes motion in 12 generalized coordinates as a function of
the externally motion. The model is based on the patellar track geometry
experimental data. The surface of the patellar track is modeled by using the
n-ellipsoid model. The inverse problem is restricted to slow motions, so we
consider that static optimization is good enough for our goal.
Keywords: knee joint
motion, surface modeling, n-ellipsoid model, patellar
track geometry, geometric and natural compatibilities.
Issue 7, Volume 7,
July 2008
Title of the Paper: Stress Strain
Modeling by Transformed Equations of Ultrasonic Wave
DOWNLOAD
FULL PDF
Authors: Arash
Ziaie, Kaveh Kumarci, Arash Kyioumarsi
Abstract: The equations of ultrasonic wave propagation in Cartesian
coordinates are functions of 27 partial displacement derivatives, which first
derived and then transformed into cylindrical coordinates. The new obtained
functions are functions of 27 partial displacements of first and second order
derivatives in cylindrical coordinates too and they will be linearized using a perturbation method based on the
Taylor series
expansion. A displacement wave, which propagates in a body, composed of two
general part; static displacement part, and also small dynamic displacement
part. Happening of the small dynamic displacement of a particle around its
static situation, Taylor
series expansion can be written around this point. Using this determined
static situation and considering only the two first components of
Taylor series
expansion, the equations of motion will be linearized.
Tremendously lengthy algebraic operations involved in the derivation and
linearization process, all of the mathematical manipulations are performed
using Mathematica.
Keywords: perturbation- acoustoelasticity- strained cylindrical solids-
ultrasonic- wave propagation- Mathematica
Title of the Paper: An Algorithm for
Clustering Tendency Assessment
DOWNLOAD
FULL PDF
Authors: Yingkang
Hu, Richard J. Hathaway
Abstract: The visual assessment of tendency (VAT) technique, developed by
J.C. Bezdek, R.J. Hathaway and J.M. Huband, uses a visual approach to find the number of
clusters in data. In this paper, we develop a new algorithm that processes
the numeric output of VAT programs, other than gray level images as in VAT,
and produces the tendency curves. Possible cluster borders will be seen as
high-low patterns on the curves, which can be caught not only by human eyes
but also by the computer. Our numerical results are very promising. The
program caught cluster structures even in cases where the visual outputs of
VAT are virtually useless.
Keywords: Clustering,
similarity measures, data visualization, clustering tendency
Title of the Paper: Computing
Exact Symmetries of Dynamical Systems from their Reduced System of Equations
can be Interesting II
DOWNLOAD
FULL PDF
Authors:
Festus I.
Arunaye
Abstract: The symmetry analysis of differential equations in the context of
Lie point and nonlocal symmetries is rich in the
literature. In this paper we present the computation of the exact symmetry
transformations of dynamical systems from their reduced systems in three
dimensions, using the Kepler problem as vehicle. We
also note that this computational technique is applicable to systems that can
be reduced to couple oscillator(s) and a conservation law.
Keywords: Exact,
symmetries, Dynamical, systems, infinitesimal, generators, flow, Kepler, Lie.
Title of the Paper: Solving the Problem
of the Compressible Fluid Flow around Obstacles by an Indirect Approach with
Vortex Distribution and Linear Boundary Elements
DOWNLOAD
FULL PDF
Authors: Luminita
Grecu
Abstract: In the present paper there is presented a solution with linear
boundary elements of lagrangean type for the
singular boundary integral equation obtained by an indirect technique with
vortex distribution for the bidimensional
compressible fluid flow around bodies. The singular boundary integral
equation the problem is reduced at is formulated in terms of primary
variables-the components of the velocity on the boundary. Numerical solutions
for the components of the velocity and the local pressure coefficient are
obtained, for different types of obstacles, with some computer codes made in
MATHCAD, based on the method exposed. For some particular cases, when
analytical solutions exist a comparison study between the numerical solutions
and the exact ones is also done. It can be seen,
from the graphics obtained, that the numerical solutions are in good
agreement with the exact solutions of the problem. The paper is also focused
on a comparison study between the numerical solutions obtained when the
indirect method with sources distribution is used and the numerical solution
presented in this paper when boundary elements of same type are used for
solving both singular boundary integral equations.
Keywords: Compressible
fluid flow, boundary element method, vortex distribution, linear boundary
elements
Title of the Paper: The
Role of Predictability of Financial Series in Emerging Market Applications
DOWNLOAD
FULL PDF
Authors: Gabriela Prelipcean,
Mircea Boscouanu, Nicolae Popoviciu
Abstract: A new metric that quantifies the predictability of financial time
series is proposed. Time series predictability provides a measure of how well
a time series can be modeled by a particular method, or how well a prediction
can be made. This new time series predictability metric is developed based on
the Kaboudan η –metric. The new metrics, based
on Genetic Programming (GP) and Artificial Neural Networks (ANN) overcomes
the stationarity problem presented in the pure
η -metric and provides a new feature, which shows how the predictability
changes over different subsequences in a time series. Timing detection and
portfolio balancing should be based on trading strategies that evolved to
optimize buy/sell decisions. The interest is to explore new trading rules
based on an automated security trading decision support system triggered by
both quantitative and qualitative factors. The focus is to develop
quantitative metrics that characterize time series according to their ability
to be modeled by a particular method, such as the predictability of a time
series using the GP approach or an ANN.
Keywords: quantitative
metrics, predictability, timing detection, portfolio selection, Genetic
Programming (GP), Artificial Neural Networks (ANN).
Title of the Paper: Mathematical
Models that Coordinate the Movement through Obstacles of the Dynamic Systems
Endowed with Artificial Sight
DOWNLOAD
FULL PDF
Authors: Ovidiu
Ilie Sandru
Abstract: This paper proposes two kinds of geometrical models meant to
coordinate the movement through obstacles of the automatons endowed with
artificial sight. Besides the novelty of theoretical nature that accompanies
them, it is important to underline the fact that these models have been
adapted to the possibilities of computer based management.
Keywords: Mathematical
modeling, dynamical system, artificial sight, motion through obstacles,
Euclidean distance, Riemann space, geodesics, Dirichlet
problem, numerical discretization.
Title of the Paper: Multiple Regression
Models of the Volumetric Stem Biomass
DOWNLOAD
FULL PDF
Authors: Noraini
Abdullah, Zainodin Jubok, Nigel Jonney J. B.
Abstract: The development of a simple model was presented for obtaining the
volumetric stem biomass of a tropical tree species. To model the volumetric
stem biomass, Cinnamomum of family Lauracea was chosen. Mensuration
data were collected based on two volumetric equations, namely, the Huber’s
and Newton’s
equations. During data collection, the variables considered were height of
stem or trunk, height of tree, diameter at breast height, diameter at middle
and diameter at top of the stem before the crown. Possible variables with
their interactions were screened with spearman correlation tests and values
greater than 0.95 were selected. The best model was determined using the
process of eight selection criteria (8SC). However, the best model was found
to be in the form of multiple regressions (MR) up to the fourth order
interactions.
Keywords: stem volume,
volumetric equations, best model, correlation tests, interactions, selection
criteria, multiple regression.
Title of the Paper: Analytical
Solutions for a Nonlinear Coupled Pendulum
DOWNLOAD
FULL PDF
Authors: Ligia
Munteanu, Veturia Chiroiu, Stefania Donescu
Abstract: In this paper, the motion of two pendulums coupled by an elastic
spring is studied. By extending the linear equivalence method (LEM), the
solutions of its simplified set of nonlinear equations are written as a
linear superposition of Coulomb vibrations. The inverse scattering transform
is applied next to exact set of equations. By using the Θ - function
representation, the motion of pendulum is describable as a linear
superposition of cnoidal vibrations and additional
terms, which include nonlinear interactions among the vibrations. Comparisons
between the LEM and cnoidal solutions and
comparisons with the solutions obtained by the fourth-order Runge-Kutta scheme are performed. Finally, an interesting
phenomenon is put into evidence with consequences for dynamic of pendulums.
Keywords: cnoidal method, linear equivalence method, cnoidal vibrations, Coulomb vibrations, coupled pendulum.
Issue 8, Volume 7,
August 2008
Title of the Paper: The Polynomial
Roots Repartition and Minimum Roots Separation
DOWNLOAD
FULL PDF
Authors: Muresan
Alexe Calin
Abstract: It is known that, if all the roots of a polynomial are real, they
can be localised, using a set of intervals, which
contain the arithmetic average of the roots. The aim of this paper is to
present an original method for giving other distributions of the roots/
modules of the roots on real axis, a method for evaluating and improving the
“polynomial minimum root separation” results, a method for the complex polynomials
and for polynomials having all roots real. We use the discriminant,
Hadamard’s inequality, Mahler’s measure and new
original inequalities. Also we will make some considerations about the cost
for isolate the polynomial real roots. Our method is based on the successive
splitting for the interval which contains all roots.
Keywords: Roots
repartition, Isolating the roots, Mahler’s measure
Title of the Paper: New Analytical Cavitation Erosion Models
DOWNLOAD
FULL PDF
Authors: Constantin
Patrascoiu
Abstract:
Cavitation erosion prediction for the hydraulic
machines is very important in the hydraulics research because that cavitation erosion is a source of failure of pumps water
turbine blade, pipelines and other hydraulic devices. In this
paper new kinds of theoretical volume loss rate curve of erosion cavitation progress is proposed. The analytical models
describing this new kind of erosion curves give a new vision of the volume
loss rate curve and produce a good concordance between the experimental and
theoretical data if there is a good choice of theoretical model. Instead of
using a unique analytical (universal) model for all materials, we give the
possibility of a good choice between the proposed models. There may also
appear some open problem such as optimally correlating this analytical cavitation erosion models with the properties of the
implied materials.
Keywords:
Cavitation, Erosion, Mathematical model,
Differential equations, Bessel’s equations.
Title of the Paper: Fully Implicit
Moving Boundary Model with Liquid Phase Perfect Mixing for CO2 Diffusion into
n-Decane
DOWNLOAD
FULL PDF
Authors: Damelys
Zabala, Aura L. Lopez De Ramos
Abstract: - Carbon dioxide diffusion into n-decane
inside cylindrical and square glass capillary tubes has been modeled [1,2], with two different models for each tube and the
convective model for the square tube depended on the results of the
cylindrical one. For those models, the liquid phase density was always
considered constant and its value was adjusted from the experimental data of
gas-liquid interface position. This approach was done using the diffusivities
obtained by correlations which modify the infinite dilution diffusion
coefficient using a thermodynamical factor. Now, the
liquid phase density is considered variable on time with perfect mixing
inside the phase and an effective diffusivity can be determined. This
effective diffusivity involves the molecular and convective contributions to
the global mass transfer. Both interface displacements (inside cylindrical
and square tubes) can be modeled using the same model without dependency
between their results. The terms inside the finite difference matrix for the
liquid phase are not constant, because they depend on the solute
concentration and on the liquid density then an iterative calculation for the
matrix coefficients must be done in each timestep. A
partially implicit model considers this iterative calculation keeping the
liquid density value for the previous time (j). A fully implicit model
considers this iterative calculation keeping the liquid density value for the
present time (j+1). It was showed that the model results, adjusted to the
experimental interface position values, predicted effective diffusivities
which are variable on time. The simulation time (76 min) for the fully implicit
numerical model is higher than the simulation time (62 min) for the partially
implicit numerical model. It was found that the type of numerical solution
scheme affects the results (up to 5% deviation) for the square capillary
model but it doesn’t change the cylindrical capillary model results.
Key-Words:
- Capillary tube, Free boundary, Mass transfer, Numerical Modeling, Diffusion.
Issue 9, Volume 7,
September 2008
Title of the Paper: An Algorithm for
Creation of an Optimized Adaptive Grid for Improved Explicit Finite Difference
Scheme
DOWNLOAD
FULL PDF
Authors: Raka Jovanovic, Milan Tuba,
Dana Simian
Abstract: This paper deals with the two main shortcomings of explicit finite
difference schemes: the use of a discretization grid with the same resolution
over the entire problem space, and low level of precision and stability. We
present a combination of two improvements. Their application is illustrated
with the numerical simulation of the propagation of a light beam in a photonic
lattice. The discretization problem is avoided by using a multi-resolution
grid. An algorithm for the grid creation is developed and that algorithm is
optimized for software implementation and parallelization. The efficiency of
the algorithm is increased by further improving the precision of the explicit
method by use of a multidimensional generalization of the Runge-Kutta scheme.
Due to the multidimensionality and nonlinearity of the considered problem, our
improved explicit finite difference gave better results than Crank-Nicholson
scheme.
Keywords: Adaptive grid algorithm, Multi-resolution, Finite differences,
Simulation, Numerical optimization
Title of the Paper: Interval-Valued
Intuitionistic Fuzzy Ideals of K-Algebras
DOWNLOAD
FULL PDF
Authors: Muhammad Akram, Karamat H. Dar,
Biao Long Meng, K. P. Shum
Abstract: The notion of interval-valued intuitionistic fuzzy sets was first
introduced by Atanassov and Gargov in 1989 as a generalization of both
interval-valued fuzzy sets and intuitionistic sets. In this paper we first
apply the concept of interval-valued intuitionistic fuzzy sets to K-algebras.
Then we introduce the notion of interval-valued intuitionistic fuzzy ideals (IIFIs,
in short) of K-algebras and investigate some interesting properties. We
characterize Artinian and Noetherian K-algebras by considering IIFIs of a
K-algebra K: Characterization theorems of fully invariant and characteristic
IIFIs are also discussed.
Keywords: K-algebras, Interval-valued intuitionistic fuzzy sets, Equivalence
relations, Artinian and Noetherian K-algebras
Title of the Paper: The Optimal Stopping
Times of American Call Options with Dividend-paying and Placing Stocks
DOWNLOAD
FULL PDF
Authors: Guangqin Li
Abstract: American options can be exercised at any time during their lifetime.
This paper addresses the optimal stopping time of several kinds of American
call options.
Keywords: Stopping time, American call option, martingale, equivalent
martingale measure, dividend-paying and placing rate
Title of the Paper: Some Preconditioning
Techniques for Linear Systems
DOWNLOAD
FULL PDF
Authors: Qingbing Liu
Abstract: New convergence intervals of parameters i are derived and applied
for solving the modified linear systems, which enables a better understanding
of how parameters should be chosen. The convergence theorem for H-matrix is
given. Meanwhile, we discuss the convergence results for M-matrices linear
systems and give some new preconditioners. Numerical examples are used to
illustrate our results.
Keywords: Convergence, H-matrix, M-matrix, Preconditioner, Gauss-Seidel method
Issue 10, Volume 7,
October 2008
Title of the Paper: The Number “6” in
Planar Tilings
DOWNLOAD
FULL PDF
Authors: Hao Li
Abstract: This paper obtains some important properties of planar normal tiling
and proves purely combinatorially Grünbaum’s Theorem. Moreover, we give the
six-neighbor-theorem and definite “relative density” to describe the increase
of tiles with some special properties. Finally, Γpm - tilings are
classified by their adjacent types.
Keywords: Normal tiling, Adjacent, Neighbor, Adjacent-graph, Relative density,
Adjacent-type
Title of the Paper: On Very True
Operators and υ-Filters
DOWNLOAD
FULL PDF
Authors: Xuejun Liu, Zhudeng Wang
Abstract: In this paper, based on Hajek, Vychodil, Rachunek and Salounova’s
works, we study the concept of υ-filters of residuated lattices with
weak υt-operators,
axiomatize very true operators, discuss filters and v-filters of residuated
lattices with weak
υt-operator, give the formulas for calculating the
υ-filters
generated by subsets, and show that lattice of
υ-filters of a
commutative residuated lattice with
υt-operator is
a complete Brouwerian lattice.
Keywords: Fuzzy logic, Residuated lattice, Very true, Weak
υt-operator,
υ-Filter
Title of the Paper: Optimal Control of a
Spin System Acting on a Single Quantum Bit
DOWNLOAD
FULL PDF
Authors: Evgenia Kirillova, Thomas Hoch,
Karlheinz Spindler
Abstract: We study a quantum spin system acting on a single quantum bit. The
evolution of this system is governed by the Schroedinger equation which takes
the form of a right-invariant system on the special unitary group SU(2) with
two control inputs. Using a suitable version of Pontryagin's Principle which
is tailor-made for control problems on Lie groups, the optimal controls are
derived in two cases: the energy-optimal case (in which the control effort is
minimized for a specified end time)and the time-optimal case (in which the
control duration is minimized for given constraints on the size of the
controls).
Keywords: Nonlinear control, optimal control, quantum spin systems
Title of the Paper: Convergence Analysis
of a Streamline Diffusion Method for a Singularly Perturbed
Convection-diffusion Problem
DOWNLOAD
FULL PDF
Authors: Zhongdi Cen, Lifeng Xi
Abstract: A streamline diffusion finite element method (SDFEM) is applied to a
singularly perturbed convection-diffusion two-point boundary value problem in
conservative form. The stability and accuracy of the SDFEM on arbitrary grids
are studied. We derive the pointwise error estimates and the approximation of
derivatives. These bounds are then made explicit for the particular cases of
Shishkin-type meshes. Numerical experiments support our theoretical results.
Keywords: Convection-diffusion, singular perturbation, streamline diffusion,
Shishkin-type mesh
Issue 11, Volume 7,
November 2008
Title of the Paper: Oscillation and
Non-oscillation Criteria for Quasi-linear Second Order Differential Equations
DOWNLOAD
FULL PDF
Authors: Wei Dong, Tieguo Ji, Xueting
Zhao
Abstract: Some oscillation and non-oscillation criteria for quasi-linear
second order equations are obtained. These results are extensions of earlier
results of C.Huang(J.Math Anal. Appl.210(1997), 712-723), A.
Elbert(J.Math.Anal.Apll.226(1998), 207-219) and
J.Wong(J.Math.Anal.Apll.291(2004), 180-188) which are all about oscillation
and non-oscillation criteria of the solution of the second order linear
equation. After the proof of the main theorem, two examples are given as the
additional remarks of the criteria. At last a special case is discussed. And
the uniqueness and periodic criteria of the special case are obtained further
by using comparison theorem and Leray-Schauder degree approach.
Keywords: Quasi-linear equation, oscillation, non-oscillations, periodic
solution, Leray-Schauder degree
Title of the Paper: Uniqueness of
Positive Solutions For Neumann Problems in Unbounded Domain
DOWNLOAD
FULL PDF
Authors: Wei Dong, Nianpeng Wang,
Chenghua Dang
Abstract:

Keywords: Sub-super solution, Neumann problem, Comparison principle, Positive
solution, Squeezing method
Title of the Paper: Reliability
Mathematics Analysis on Traction Substation Operation
DOWNLOAD
FULL PDF
Authors: Hongsheng Su
Abstract: In electrified railway traction power supply systems, the
operational qualities and reliabilities of the main traction transformer loop
is higher, but ones of bus output units is comparatively low. The traction
transformer loop still works when output loops are in failure, and the output
loop interrupts working when the main transformer is in failure, and only has
residual life when restoring working, the connection formation between them is
in series. Traditional reliability analysis methods let their lifetime follow
exponential distribution, and reliability is investigated based on the minimal
path sets, which lead to a comparatively rough result, consequently. According
to Markov theory, in this paper the main loop life is considered as mixed
Erlang distribution with order n, and the output unit life follows generic
distribution. As compared with conventional series systems, the acquired
results are proved to be reliable and sound.
Keywords: Transformer, Erlang distribution, Life, Markov theory, Reliability,
Traction substation
Title of the Paper: Indeterminate Forms
and their Behaviours
DOWNLOAD
FULL PDF
Authors: Saeed Al-Hajjar
Abstract: This study shows that there exist solutions to the seven main
indeterminate forms that are raised in the world of mathematics. Some limits
of functions are said to be indeterminate when merely knowing the limiting
behaviour of individual parts of expression is not sufficient to actually
determine the overall limit. There will be a study of a certain typical number
whereas, if a variable x tends to a certain value α (eventually equal to +∞ or
-+∞)
, a certain function Γ(x) does not have an apparent limit from the first view.
To eliminate the indetermination (or looking for the right value of
Γ(α), is to find this
limit if it exists.
Keywords: Infinity , indeterminate, equivalent infinitely large principal,
equivalent infinitely small principal, limit, function
Title of the Paper: Particle Swarm
Optimization – Tabu Search Approach to Constrained Engineering Optimization
Problems
DOWNLOAD
FULL PDF
Authors: Ritchie Mae Gamot, Armacheska
Mesa
Abstract: Constraint handling is one of the most difficult parts encountered
in practical engineering design optimizations. Different kinds of methods were
proposed for handling constraints namely, genetic algorithm, self-adaptive
penalty approach and other evolutionary algorithms. Particle Swarm
Optimization (PSO) efficiently solved most nonlinear optimization problems
with inequity constraints. This study hybridizes PSO with a meta-heuristic
algorithm called Tabu Search (TS) to solve the same engineering design
problems. The algorithm starts with a population of particles or solution
generated randomly and is updated using the update equations of PSO. The
updated particles are then subjected to Tabu Search for further refinement.
The PSO algorithm handles the global search for the solution while TS
facilitates the local search. With embedded hyrbridization, this study which
we call PSO-TS, showed better results compared to algorithms reported in Hu et
al's study as applied to four benchmark engineering problems. Specifically,
this study beat the results of Coello, Deb and Hu.
Keywords: Constrained engineering optimization problems, particle swarm
optimization, tabu search
Issue 12, Volume 7,
December 2008
Title of the Paper: Optimal Control of a
Spin System Acting on a Single Quantum Bit
DOWNLOAD
FULL PDF
Authors: Evgenia Kirillova, Thomas Hoch,
Karlheinz Spindler
Abstract: We study a quantum spin system acting on a single quantum bit. The
evolution of this system is governed by the Schr¨odinger equation which takes
the form of a right-invariant system on the special unitary group SU(2) with
two control inputs. Using a suitable version of Pontryagin’s Principle which
is tailor-made for control problems on Lie groups, the optimal controls are
derived in two cases: the energy-optimal case (in which the control effort is
minimized for a specified end time) and the time-optimal case (in which the
control duration is minimized for given constraints on the size of the
controls).
Keywords: Nonlinear control, optimal control, quantum spin systems
Title of the Paper: Peak-Valley
Segmentation Algorithm for Fatigue Time Series Data
DOWNLOAD
FULL PDF
Authors: Z. M. Nopiah, M. I. Khairir, S.
Abdullah, C. K. E. Nizwan
Abstract: This paper presents the peak-valley (PV) segmentation algorithm for
the purpose of producing a reliable method of fatigue time series segmentation
and statistical segment-by-segment analysis of fatigue damage. The time series
were segmented using a piecewise linear representation (PLR) based
segmentation algorithm and consecutively the peak-valley (PV) segmentation
algorithm. Statistical analysis and fatigue damage calculations were made on
each segment and scatter plots were produced based on the relationship between
segmental damage and its corresponding kurtosis value. Observations were made
on the scatter plots produced by the PV segmentation algorithm to determine
the reliability of the data scattering for fatigue data clustering prospects.
Keywords: Time series, segmentation, peak-valley, data scattering, kurtosis,
fatigue damage
Title of the Paper: Abrupt Changes
Detection in Fatigue Data Using the Cumulative Sum Method
DOWNLOAD
FULL PDF
Authors: Z. M. Nopiah, M. N.Baharin, S.
Abdullah, M. I. Khairir, C. K. E. Nizwan
Abstract: The detection of abrupt changes refers to a time instant at which
properties suddenly change, but before and after which properties are constant
in some sense. CUSUM (Cumulative Sum) is a sequential analysis technique that
is used in the detection of abrupt changes. The objective in this study is to
apply CUSUM technique in analysing fatigue data for detection of abrupt
changes. For the purpose of this study, a collection of nonstationary data
that exhibits a random behavior was used. This random data was measured in the
unit of microstrain on the lower suspension arm of a car. Experimentally, the
data was collected for 60 seconds at a sampling rate of 500 Hz, which gave
30,000 discrete data points. By using CUSUM method, a CUSUM plot was
constructed in monitoring the mean changes for fatigue data. Global signal
statistical value indicated that the data were non Gaussian distribution in
nature. The result of the study indicates that CUSUM method is only applicable
for certain type of data with mixed high amplitude in a random background
data.
Keywords: Abrupt changes, CUSUM, nonstationary data, mean changes, global
statistics
Title of the Paper: The Suitability of
Statistical Distribution in Fitting Wind Speed Data
DOWNLOAD
FULL PDF
Authors: Azami Zaharim, Siti Khadijah
Najid, Ahmad Mahir Razali, Kamaruzzaman Sopian
Abstract: Wind energy has been used for navigation and agriculture. Recently,
wind energy is given a lot of attention because of the focus on renewable
energy. Wind energy growth in Asia is currently on the rise. Both India and
China are leading with more installed capacity and manufacturing facilities.
In Malaysia, wind energy conversion is also given a serious consideration. The
potential for wind energy generation in Malaysia depends on the availability
of the wind resource that varies with specific location. This paper deals with
how to model or how to fit several probability distribution models to Malaysia
wind speed data available. As usually described in the literature concerning
efforts to develop an adequate statistical model for wind speed, there are a
few statistical models discussed such as Weibull Distribution and Rayleigh
Distribution. In the literature, it is a common procedure to compare these
functions to determine which one fits the measured distribution best. The
result from a simple descriptive statistics shows that Weibull distribution
might be the probability distribution that can fit the data well.
Keywords: Wind speed, wind speed distribution, Weibull
|



