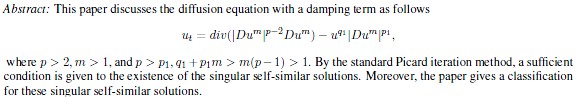|
Issue 1, Volume 11,
January 2012
Title of the Paper: Bipartite Theory of
Semigraphs
DOWNLOAD
FULL PDF
Authors: Y. B.
Venkatakrishnan, V. Swaminathan
Abstract: Given a semigraph, we can construct graphs Sa, Sca, Se and S1e. In
the same pattern, we construct bipartite graphs CA(S), A(S), VE(S), CA+(S) and
A+(S). We find the equality of domination parameters in the bipartite graphs
constructed with the domination and total domination parameters of the graphs
Sa and Sca. We introduce the domination and independence parameters for the
bipartite semigraph. We have defined Xachromatic number, Xa-hyperindependent
number and Xa-irredundant number. Using these parameters, we have defined a
Xa-dominating sequence chain.
Keywords: Semigraph,
Xa-dominating set, Ya-dominating set, Xa-independent set, Xa-hyperindependent
set, hyper Xa-independent set
Title of the Paper: Parameter
Estimation and Cooperative Effects in Queueing Networks
DOWNLOAD
FULL PDF
Authors: Gurami
Tsitsiashvili, Marina Osipova
Abstract: This paper is devoted to probability-statistical analysis of
Jackson opened and closed networks. A prob- lem of an estimation of product
limit distributions parameters using load coefficients of network nodes is
solved. Cooperative effects in aggregated opened and closed networks are
investigated and optimization procedures of their limit deterministic
characteristics are constructed. Formulas of a calculation of limit
distributions in superpositions of networks (nodes are replaced by opened
networks) are obtained.
Keywords: Phase
transition, aggregated networks, superposition of networks, product limit
distributions, load coefficients, limit characteristics, parameters estimation
Title of the Paper: Computing Rupture
Degrees of Some Graphs
DOWNLOAD
FULL PDF
Authors: Fengwei Li,
Qingfang Ye, Baohuai Sheng
Abstract: Computer or communication networks are so designed that they do not
easily get disrupted under ex- ternal attack and, moreover, these are easily
reconstructed when they do get disrupted. These desirable properties of
networks can be measured by various parameters such as connectivity,
toughness, tenacity and rupture degree. Among these parameters, rupture degree
is comparatively better parameter to measure the vulnerability of net- works.
In this paper, the authors give the exact values for the rupture degree of the
Cartesian product of a path and a cycle. After that, we discuss the rupture
degree of total graphs of paths and cycles. Finally, we study the values for
rupture degree of powers of paths and cycles.
Keywords: Rupture degree,
Vulnerability, Cartesian product, Total graph, Powers of graphs, R-set
Title of the Paper: A New Iterative
Method for Equilibrium Problems, Fixed Point Problems of Infinitely
Nonexpansive Mappings and a General System of Variational Inequalities
DOWNLOAD
FULL PDF
Authors: Jing Zhao,
Caiping Yang, Guangxuan Liu
Abstract: In this paper, we introduce a new iterative scheme for finding the
common element of the set of common fixed points of infinitely many
nonexpansive mappings, the set of solutions of an equilibrium problem and the
set of solutions of a general system of variational inequalities for
inverse-strongly monotone mappings in Hilbert spaces. We prove that the
sequence converges strongly to a common element of the above three sets under
some parameters controlling conditions. This main result improve and extend
the corresponding results announced by many others. Using this theorem, we
obtain three corollaries.
Keywords: Nonexpansive
mapping, Equilibrium problem, Fixed point, Inverse-strongly monotone mapping,
General system of variational inequality, Iterative algorithm
Title of the Paper: Two New
Constructions of Multi-receiver Authentication Codes from Singular
Pseudo-Symplectic Geometry over Finite Fields
DOWNLOAD
FULL PDF
Authors: Gao You, Chang
Liwei
Abstract: In this paper, two new constructions of multi-receiver
authentication codes using singular pseudo- symplectic geometry on finite
fields are described. Under the assumption that the encoding rules of the
transmitter and the receiver are chosen according to a uniform probability
distribution, the parameters and the probabilities of success for different
types of deceptions are computed by the method of matrix and combinatorial
enumeration.
Keywords: Multi-receiver
authentication codes, Singular pseudo-symplectic geometry, Finite fields,
Construction, Combinatorial enumeration
Title of the Paper: Two Constructions
of Multireceiver Authentication Codes from Singular Symplectic Geometry over
Finite Fields
DOWNLOAD
FULL PDF
Authors: Chen Shangdi,
An Lei
Abstract: Multireceiver authentication codes allow one sender to construct an
authenticated message for a group of receivers such that each receiver can
verify authenticity of the received message. In this paper, two constructions
of multireceiver authentication codes from singular symplectic geometry over
finite fields are given. The parameters and the probabilities of success for
different types of deceptions are computed.
Keywords: Singular
symplectic geometry, Multireceiver authentication codes, Finite fields,
Construction, Probability
Title of the Paper: Periodic Traveling
Wave Solutions for a Coupled Map Lattice
DOWNLOAD
FULL PDF
Authors: Mei-Feng Li,
Guang Zhang, Hui-Feng Li, Jin-Liang Wang
Abstract: A type of coupled map lattice (CML) is considered in this paper.
What we want to do is to define the form of a traveling wave solution and to
reveal its existence. Due to the infinite property of the problem, we have
tried the periodic case, which can be dealt with on a finite set. The main
approach for our study is the implicit existence theorem. The results indicate
that if the parameters of the system satisfy some exact conditions, then there
exists a periodic traveling wave solution in an exact neighborhood of a given
one. However, these conditions are sufficient, but not necessary. In
particular, the exact 2-periodic traveling wave solutions are also obtained.
It gives some examples for the conditions of parameters, 2-periodic traveling
wave solutions exist when these conditions are satisfied.
Keywords: Coupled map
lattice, Periodic traveling wave solution, Implicit existence theorem, Nagumo
equation, Nontrivial solution
Title of the Paper: Dynamics of
Stage-structured Population Models with Harvesting Pulses
DOWNLOAD
FULL PDF
Authors: Li Changguo
Abstract: In most models of population dynamics, changes in population due to
birth or harvesting are assumed to be time-independent, but many species
reproduce or are caught only during a single period of the year. In this paper
a single species stage-structured model with density-dependent maturation
rate, birth pulse and harvesting pulse is formulated. Using the discrete
dynamical system determined by its Poincare map, the existence and stability
of nonnegative equilibrium is studied. Furthermore by simulation, a detailed
study of the various dynamics are made including period doubling, period
halfing, intermittency, crisis, nonunique dynamics and chaotic attractors. The
occurrence of these complex dynamic behaviors is related to the fact that
minor changes in parameter or initial values can strikingly change the dynamic
behaviors of the system. Finally, the dynamic behavior of the system is
compared when ì is used as a bifurcation parameter with that when b is used.
Keywords: Stage
structure, Density-dependent, Harvesting pulse, Birth pulse, Complexities
Issue 2, Volume 11,
February 2012
Title of the Paper: New Hybrid Steepest
Descent Algorithms for Variational Inequalities over the Common Fixed Points
Set of Infinite Nonexpansive Mappings
DOWNLOAD
FULL PDF
Authors: He Songnian,
Sun Wenwen
Abstract: New hybrid steepest descent algorithms which are different from
Yamada’s hybrid steepest descent algorithms are proposed for solving
variational inequalities defined on the common fixed points set of infinite
nonexpansive mappings. As the extensions of our main results , algorithms are
also given for solving variational inequalities defined on the common fixed
points set of infinite ê-strict pseudo-contractions.
Keywords: Hilbert space,
fixed point, nonexpansive mapping, strict pseudo-contraction, variational
inequality, hybrid steepest descent algorithm
Title of the Paper: Study on the
Periodic Solution and Invariant Tori for Iced Cable
DOWNLOAD
FULL PDF
Authors: Jing Li,
Xiaoli Wei
Abstract: In this paper, the behavior of iced cable with two degrees of
freedom is investigated. With Melnikov function of the system, the sufficient
condition for the existence of periodic solutions about the system is
obtained. The invariant tori of the system is investigated by using
transformations and average equation. The conclusion not only enriches the
behavior of nonlinear dynamics about iced cable, but also provides the
reference to the study of controlling the icing disaster, which is caused by
large amplitude low frequency vibration of iced cable.
Keywords: Iced Cable,
periodic solution, invariant torus, Melinkov function, transformation
Title of the Paper: Global Solutions
for Second Order Impulsive Integro-Differential Equations in Banach Spaces
DOWNLOAD
FULL PDF
Authors: Wang Xinfeng,
Liu Dalian, Li Chong
Abstract: This paper regards initial value problem for second order impulsive
integro-differential equations as some nonlinear vector system. By means of
the M¨onch′s fixed point theorem, some existence theorems of solu- tions of
the initial value problem are established. The results are newer than all of
the previous ones because of the more general form compactness-type condition
and the weaker restriction of its coefficients. An example is given to
demonstrate our results. Annotation shows that our method can be used to solve
the impulsive boundary value problems.
Keywords: Impulsive
integro-differential equations, initial value problem, Boundary value problem,
Compactness-type condition, Banach space, Fixed point, Operator norm of the
matrix
Title of the Paper: Application of an
Improved Adaptive Chaos Prediction Model in Aero-Engine Performance Parameters
DOWNLOAD
FULL PDF
Authors: Chunxiao
Zhang, Junjie Yue
Abstract: Based on the research of complexity and non-linearity of
aero-engine exhaust gas temperature (EGT) system, a regularization adaptive
chaotic prediction model applied in short time forecasting of EGT was
proposed. In this research, we develop a new hybrid particle swarm
optimization (HPSO) arithmetic in order to improve the accuracy of the
forecasting model. This arithmetic enhanced the ability of dealing with
integer variables and constraints by adding and changing some manipulations to
fit in with optimizing continuous and integer variables. The test results are
based on QAR data supplied by a civil airline company, and show that the
proposed framework performs better than the traditional chaotic forecasting
model on prediction accuracy. Therefore, this arithmetic is efficient and
feasible for a short-term prediction of aero-engine exhaust gas temperature.
Keywords: Exhaust gas
temperature (EGT), Regularization, Adaptive chaos prediction, Hybrid particle
swarm optimization (HPSO), Principal component regression(PCR), Aero-engine
Title of the Paper: The Singular
Diffusion Equation with Boundary Degeneracy
DOWNLOAD
FULL PDF
Authors: Qingmei Xie,
Huashui Zhan
Abstract: For the heat conduction on a bounded domain with boundary
degeneracy, though its diffusion coefficient vanishes on the boundary, it is
still possible that the heat flux may transfer across the boundary. A known
result shows that the key role is the ratio of the diffusion coefficient near
the boundary. If this ratio is large enough, the heat flux transference has
not any relation to the boundary condition but is completely controlled by the
initial value. This phenomena shows there are some essential differences
between the heat flux with boundary degeneracy and that without boundary
degeneracy. However, under the assumption on the uniqueness of the weak
solutions, the paper obtains that the weak solution of the singular diffusion
equation with boundary degeneracy, has the same regular properties as the
solution of a singular diffusion equation without boundary degeneracy.
Keywords: Boundary
degeneracy, Diffusion equation, Uniqueness, Regular property
Title of the Paper: Some Boundary
Properties of Cauchy Type Integral in Terms of Mean Oscillation
DOWNLOAD
FULL PDF
Authors: Rahim M.
Rzaev, Aysel B. Imanova
Abstract: In this paper radial boundary values of Cauchy type integral are
investigated when conditions on integral density are set in terms of mean
oscillation of functions. Corresponding statements about boundary values of
Poisson integral and conjugate Poisson integral are proved.
Keywords: Cauchy type
integral, Poisson integral, boundary values, singular integrals, mean
oscillation
Title of the Paper: Introduction to the
Angular Functions in Euclidian 2D-space
DOWNLOAD
FULL PDF
Authors: Claude Ziad
Bayeh
Abstract: The Angular functions are new mathematical functions introduced by
the author, they produce rectangular signals, in which period is function of
angles and not of time as the previous functions. Similar to trigonometric
functions, the angular functions have the same properties as the precedent,
but the difference is that a rectangular signal is obtained instead of a
sinusoidal signal, and moreover, one can change the width of each positive and
negative alternate in the same period. This is not the case of any other
trigonometric function. In other hand, one can change the frequency, the
amplitude and the width of any period of the signal at any position by using
the general form of the angular function. In this paper, an original study is
introduced. Thus, the definition of the original part is presented. The
angular functions are also defined. These functions are very important in
technical subjects. They will be widely used in mathematics and in engineering
domains, especially in power electronics, signal theory, propagation of
signals and many other topics. Moreover, the Angular functions are the basis
of the Elliptical trigonometry and the rectangular trigonometry in which they
are new domains introduced in mathematics by the author.
Keywords: Mathematics,
geometry, trigonometry, pulse width modulation, signal theory, power
electronics
Title of the Paper: Introduction to the
General Trigonometry in Euclidian 2D-Space
DOWNLOAD
FULL PDF
Authors: Claude Ziad
Bayeh
Abstract: The General Trigonometry is a new trend of trigonometry introduced
by the author into the mathematical domain. It is introduced to replace the
traditional trigonometry; it has huge advantages ahead the traditional one. It
gives a general concept view of the trigonometry and forms an infinite number
of trigonometry branches and each branch has its own characteristics and
features. The concept of the General Trigonometry is completely different from
the traditional one in which the study of angles will not be the relation
between sides of a right triangle that describes a circle as the previous one,
but the idea here is to use the relation between angles and sides of a
geometrical form (e.g.: circle, elliptic, rectangle, quadrilateral …) with the
internal and external circles formed by the intersection of the geometrical
form and the positive parts of x’ox and y’oy axis in the Euclidian 2D space
and their projections. This new concept of relations will open a huge gate in
the mathematical domain and it can resolve many complicated problems that are
difficult or almost impossible to solve with the traditional trigonometry, and
it can describe a huge number of multi form periodic signals. The most
remarkable trigonometry branches are the “Elliptical trigonometry” and the
“Rectangular trigonometry” introduced by the author and published by WSEAS.
The importance of these trigonometry branches is that with one function, we
can produce multi signal forms by varying some parameters. In this paper, an
original study is introduced and developed by the author and some few examples
are discussed only to give an idea about the importance of the General
Trigonometry and its huge application in all scientific domains especially in
Mathematics, Power electronics, Signal theory and processing and in Energy
Economic Systems.
Keywords: Modern
mathematics, trigonometry, angular function, multi form signal, power
electronics
Issue 3, Volume 11,
March 2012
Title of the Paper: A Formulation of
Conditional States on Steganalysis Approach
DOWNLOAD
FULL PDF
Authors: Roshidi Din,
Zhamri Che Ani, Azman Samsudin
Abstract: In this paper, we present a consolidated formulation of conditional
states from the perspective of steganalysis approach. It has been identified
that the conditional states used in steganalysis approach include hypothesis
testing, gaussion distribution, hidden markov model and vector analysis space.
The main objective of this paper is to find the best approach to fit in using
mathematical formulation for steganalytic system based on these conditional
states. It is found that there is a boundary of solution between the
steganalytic system and analyzed message.
Keywords: Steganalysis,
Steganalytic System, Steganography
Title of the Paper: First Order
Unstructured Algorithms Applied to the Solution of the Euler Equations in
Three-Dimensions
DOWNLOAD
FULL PDF
Authors: Edisson Sávio
de Góes Maciel
Abstract: In the present work, the Roe, the Steger and Warming, the Van Leer,
the Harten, the Frink, Parikh and Pirzadeh, the Liou and Steffen Jr. and the
Radespiel and Kroll schemes are implemented, on a finite volume context and
using an upwind and unstructured spatial discretization, to solve the Euler
equations in the three-dimensional space. The Roe, the Harten, and the Frink,
Parikh and Pirzadeh schemes are flux difference splitting ones, whereas the
others schemes are flux vector splitting ones. All seven schemes are first
order accurate in space. The time integration uses a Runge-Kutta method and is
second order accurate. The physical problems of the supersonic flow along a
ramp and the “cold gas” hypersonic flow along a diffuser are solved. The
results have demonstrated that the Liou and Steffen Jr. scheme is the most
conservative algorithm among the studied ones, whereas the Van Leer scheme is
the most accurate.
Keywords: Flux difference
splitting algorithms, Flux vector splitting algorithms, Unstructured schemes,
Euler equations, Three-Dimensions, Supersonic and hypersonic flows
Title of the Paper: The Solutions of
Initial Value Problems for Nonlinear Fourth-Order Impulsive
Integro-Differential Equations in Banach Spaces
DOWNLOAD
FULL PDF
Authors: Zhang
Lingling, Yin Jingyi, Liu Junguo
Abstract: In this paper, we investigate the maximal and minimal solutions for
initial value problem of fourth order impulsive differential equations by
using cone theory and the monotone iterative method to some existence results
of solution are obtained. As an application, we give an example to illustrate
our results.
Keywords: Banach space,
Cone, Initial value problem, Impulsive integro-differential equations
Title of the Paper: Optimal Design of
Circular Plates with Internal Supports
DOWNLOAD
FULL PDF
Authors: Jaan Lellep,
Julia Polikarpus
Abstract: The behaviour of circular plates with internal rigid ring supports
is investigated. The material of plates is assumed to be an ideal elastic
material obeying the Hooke’s law. The case of an elastic circular plate
supported at the edge and resting on an absolutely rigid ring support is
studied in a greater detail. Various optimization problems with unknown
positions of extra supports are discussed and the problem of optimal location
of the internal support is solved under the condition that the cost of the
support is proportional to its length. Making use of the variational methods
of the optimal control theory necessary conditions of optimality are deduced
analytically. Numerical results are presented for the case of uniformly
distributed transverse pressure.
Keywords: plate, internal
support, optimization, optimal control
Title of the Paper: Distribution of the
Maximum Costs of Products in Direct Selling
DOWNLOAD
FULL PDF
Authors: Li-Fei Huang
Abstract: Direct selling companies do not reveal the cost of their products
and typically design complex rules for their employees regarding commission.
Therefore, determining how much an employee offers to other multilevel above
employees is difficult. This study selects one direct selling company to
investigate the rules of commission. However, knowing the product costs may
assist us in selecting an appropriate choice from among the numerous direct
selling companies. Statistical knowledge is used to develop a
binomial-geometric model for the complicated commission rules. Using this
model, the probability distribution is proved and the mean and standard
deviation percentages of cost are found for all employees according to the
employee proportions in all stages of the two examples. Employees in lower
stages must pay more commission to multilevel above employees, particularly in
companies with few top employees. Obtaining sufficient employees to earn
commission from the low-cost direct selling product is challenging. Therefore,
employees should individually judge whether the direct selling products are
worth purchasing and selling.
Keywords: Applied
probability, Binomial-geometric distribution, Direct selling, Upgrading and
commission rules, Proportion of commission, Distribution of maximum product
cost
Title of the Paper: Optimization of
Conical Shells of Piece Wise Constant Thickness
DOWNLOAD
FULL PDF
Authors: Jaan Lellep,
Ella Puman
Abstract: Conical shells with piece wise constant thickness subjected to the
distributed transverse pressure and loaded by a rigid central boss are
studied. In the paper the both, elastic and inelastic shells are considered.
In the case of inelastic shells it is assumed that the material obeys the
Hill’s plasticity condition and associated flow rule. The optimization problem
is posed in a general form involving as particular cases several different
problems. Resorting to the variational methods necessary optimality conditions
are derived. The problems regarding to the maximization of the plastic limit
load and to the minimum weight design are studied in a greater detail.
Keywords: thin walled
shell, optimal design, yield condition, associated flow law, elasticity
Title of the Paper: Positive Solutions
of Operator Equations and Nonlinear Beam Equations with a Perturbed Loading
Force
DOWNLOAD
FULL PDF
Authors: Wen-Xia Wang,
Xi-Lan Liu
Abstract: In this paper we are concerned with the existence and uniqueness of
positive solutions for an operator equation x = Ax + ëBx on an order Banach
space, where A and B are nonlinear operators and ë is a parameter. By
properties of cones we obtain that there exists a ë* > 0 such that
the operator equation has a unique positive solution which is increasing in ë
for ë є [0,
ë*], and further, we give an estimate for ë*. In
addition, we discuss the existence and uniqueness of positive solutions for an
elastic beam equation with three parameters and one perturbed loading force.
Keywords: Nonlinear
operator equation; positive solution; elastic beam equation; perturbed loading
force
Title of the Paper: Reentry Flows in
Chemical Non-Equilibrium in Three-Dimensions
DOWNLOAD
FULL PDF
Authors: Edisson Sávio
De Góes Maciel, Amilcar Porto Pimenta
Abstract: This work presents a numerical tool implemented to simulate inviscid
and viscous flows employing the reactive gas formulation of thermal
equilibrium and chemical non-equilibrium in three-dimensions. The Euler and
Navier-Stokes equations, employing a finite volume formulation, on the context
of structured and unstructured spatial discretizations, are solved. These
variants allow an effective comparison between the two types of spatial
discretization aiming verify their potentialities: solution quality,
convergence speed, computational cost, etc. The aerospace problem involving
the hypersonic flow around a blunt body, in three-dimensions, is simulated.
The reactive simulations will involve an air chemical model of five species:
N, N_2, NO, O and O_2. Seventeen chemical reactions, involving dissociation
and recombination, will be simulated by the proposed model. The Arrhenius
formula will be employed to determine the reaction rates and the law of mass
action will be used to determine the source terms of each gas species
equation.
Keywords: Euler and
Navier-Stokes equations, Reactive formulation, Chemical non-equilibrium,
Hypersonic flow, Van Leer algorithm, Three-dimensions
Issue 4, Volume 11,
April 2012
Title of the Paper: New Families of
Eighth-Order Methods with High Efficiency Index for Solving Nonlinear
Equations
DOWNLOAD
FULL PDF
Authors: Lingling Zhao,
Xia Wang, Weihua Guo
Abstract: In this paper, we construct two new families of eighth-order methods
for solving simple roots of non- linear equations by using weight function and
interpolation methods. Per iteration in the present methods require three
evaluations of the function and one evaluation of its first derivative, which
implies that the efficiency indexes are 1.682. Kung and Traub conjectured that
an iteration method without memory based on n evaluations could achieve
optimal convergence order 2n−1. The new families of eighth-order methods agree
with the conjecture of Kung-Traub for the case n = 4. Numerical comparisons
are made with several other existing methods to show the performance of the
presented methods, as shown in the illustration examples.
Keywords: Eighth-order
convergence, Nonlinear equations, Weight function methods, Convergence order,
Efficiency index
Title of the Paper: On Using the He’s
Polynomials for Solving the Nonlinear Coupled Evolution Equations in
Mathematical Physics
DOWNLOAD
FULL PDF
Authors: E. M. E. Zayed,
H. M. Abdel Rahman
Abstract: In this article, we apply the modified variational iteration method
for solving the (1+1)- dimensional Ra- mani equations and the
(1+1)-dimensional Joulent Moidek (JM) equations together with the initial
conditions. The proposed method is modified the variational iteration method
by the introducing He’s polynomials in the correction functional. The
analytical results are calculated in terms of convergent series with easily
computated components.
Keywords: Variational
iteration method, Homotopy perturbation methods, Coupled nonlinear evaluation
equations, Exact solutions
Title of the Paper: Some Ostrowski Type
Inequalities On Time Scales Involving Functions of Two Independent Variables
DOWNLOAD
FULL PDF
Authors: Qinghua Feng,
Fanwei Meng
Abstract: In this paper, we establish some new Ostrowski type inequalities on
time scales involving functions of two independent variables for multiple
points, which unify continuous and discrete analysis, and some of which are
sharp. The established results extend some known results in the literature,
and can be used in the estimate of error bounds for some numerical quadrature
formulae.
Keywords: Ostrowski type
inequality, Time scales, Numerical integration, Error bound, Sharp bound
Title of the Paper: Existence and
Iterative Algorithm of Solutions for a New System of Generalized Set-Valued
Mixed Equilibrium-Like Problems in Banach Spaces
DOWNLOAD
FULL PDF
Authors: De-Ning Qu,
Cao-Zong Cheng
Abstract: A new system of generalized set-valued mixed equilibrium-like
problems (in short, S-GMELP) in Ba- nach spaces is discussed. In order to
obtain the existence of solutions of S-GMELP, a system of related auxiliary
problems (in short, S-AP) is established. On the basis of the existence and
uniqueness of solutions of the S-AP, an iterative algorithm for the S-GMELP is
constructed. It is proved that the iterative sequence converges some solution
of S-GMELP. Finally, an example is given to well exemplify our main result.
Keywords: Equilibrium-like
problem, Auxiliary principle technique, Existence, Iterative algorithm, Banach
space
Title of the Paper: Convolutional Codes
Under Linear Systems Point of View. Analysis of Output-Controllability
DOWNLOAD
FULL PDF
Authors: M. I.
Garcia-Planas, El M. Souidi, L. E. Um
Abstract: In this work we make a detailed look at the algebraic structure of
convolutional codes using techniques of linear systems theory. In particular
we study the input-state-output representation of a convolutional code. We
examine the output-controllability property and we give conditions for this
property. At the end of the paper is presented a brief introduction to the
analysis of output controllability for parallel concatenated codes.
Keywords: Codes, linear
systems, output-controllability
Title of the Paper: A Study on the
Complexity of Multi-Enterprise Output Game in Supply Chain
DOWNLOAD
FULL PDF
Authors: Guanhui Wang,
Junhai Ma
Abstract: Based on an analysis on a variety of game models in the supply
chain, this paper proposes a multi-enterprise output game model under the
circumstances of information asymmetry. After a study on Nash equilibrium, the
paper analyzes the factors that cause chaos in production decision making
among manufacturers and offers numerical simulation. The authors argue that
under the circumstances of information asymmetry, the differences in
productivity adjustment factor exert great impact on the manufacturers, shown
as bifurcation and chaos, whereas the distributors and retailers are scarily
affected. The measures to keep the chaos among manufacturers are suggested.
Keywords: supply chain,
output game, bifurcation, Lyapunov exponents, discrete dynamical system,
complexity
Title of the Paper: The Self-Similar
Solutions of a Diffusion Equation
DOWNLOAD
FULL PDF
Authors: Huashui Zhan
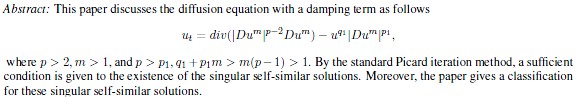
Keywords: Diffusion
equation, Damping term, Picard iteration method, Self-similar solution,
Singular solution
Title of the Paper: Introduction to the
General Trigonometry in Euclidian 2D-Space
DOWNLOAD
FULL PDF
Authors: Claude Ziad
Bayeh
Abstract: The General Trigonometry is a new trend of trigonometry introduced
by the first author into the mathematical domain. It is introduced to replace
the traditional trigonometry; it has huge advantages ahead the traditional
one. It gives a general concept view of the trigonometry and forms an infinite
number of trigonometry branches and each branch has its own characteristics
and features. The concept of the General Trigonometry is completely different
from the traditional one in which the study of angles will not be the relation
between sides of a right triangle that describes a circle as the previous one,
but the idea here is to use the relation between angles and sides of a
geometrical form (e.g.: circle, elliptic, rectangle, quadrilateral …) with the
internal and external circles formed by the intersection of the geometrical
form and the positive parts of x’ox and y’oy axis in the Euclidian 2D space
and their projections. This new concept of relations will open a huge gate in
the mathematical domain and it can resolve many complicated problems that are
difficult or almost impossible to solve with the traditional trigonometry, and
it can describe a huge number of multi form periodic signals. The most
remarkable trigonometry branches are the “Elliptical trigonometry” and the
“Rectangular trigonometry” introduced by the author and published by WSEAS.
The importance of these trigonometry branches is that with one function, we
can produce multi signal forms by varying some parameters. In this paper, an
original study is introduced and developed by the author and some few examples
are discussed only to give an idea about the importance of the General
Trigonometry and its huge application in all scientific domains especially in
Mathematics, Power electronics, Signal theory and processing and in Energy
Economic Systems.
Keywords: Modern
mathematics, trigonometry, angular function, multi form signal, power
electronics
|